三角形と四角形っす

もうPrimToTextのままで行くっす。

良い名前も浮かばないっすからね。

どうもぺんぎんっす( ◎v◎ )

ボックスに穴形状:三角形で中空を入れた場合、

プリズムに穴形状:正方形で中空を入れた場合、

頂点の結び方が悩ましいっす。

三角形と四角形になるっすからね。

ボックスに三角形の穴をあける場合を考えるとき、

内側の三角形はパスカットをイメージすると良いっす。

頂点の位置はボックスに1/3(≒0.333)、2/3(≒0.667)の

パスカットを設定したときのボックスの断面上にあるっす。

つまりこういうことっす。

説明しやすいように名前も付けたっす。

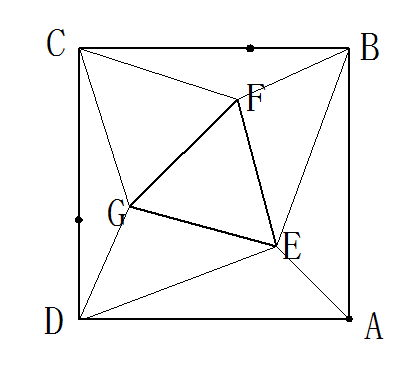
補助線がいっぱい出てるっすけど、それらは垂直二等分線っす。

特に三角形の各辺の垂直二等分線と四角形の辺との交点は

黒丸を付けたっす。FGの垂直二等分線はAを通るので

辺ではないっすけどね。

上の図から何が分かるかと言うと、

「E、F、Gの各頂点から一番近い頂点はA、B、C、Dのうちどれ？」

っていうのが分かるっす。

垂直二等分線を引いたのはこのためっす。

EはAが一番近く、

FはBが一番近く、

GはDが一番近い、

となるっす。

これからやることは、穴あき正方形を三角形に区切ることっす。

いわゆる三角ポリゴンってやつっす。

まずは近いもの、AE、BF、DGを結ぶっす。

Cは余ったので、CF、CGと結んでおくっす。

残りは四角形AEGDと四角形ABFEの部分っす。

四角形AEGDは「AGとDE、短いのはどっち？」で、短い方を選択するっす。

四角形ABFEも同様に「AFとBE、短いのはどっち？」をやるっす。

自分は図を書いてCADで計測するズルをしたんっすけど、

良い子は頑張って計算してくださいっす。

図のような7つの三角形になるっす。

PrimToTextでもこんな風に分割してやるっすよ。